Kasutaja:Asaidlo/Rubiku kuubiku õpik/Kiht-kihi haaval lahendamine

Järgnevas peatükis hakkame päriselt Rubiku kuubikut lahendama. Selle jaoks kasutame suhteliselt levinud algajate meetodit. Kõigepealt loome ühele küljele risti, saajärel lõpetame esimese kihi, lahendades nurgad. Teise kihi lahendamiseks peame paigutama õigetesse asukohtadesse neli ääretükki. Lõpetuseks orienteerime ja permuteerime viimase kihi tükid.

Enne lahendamist lepime kokku, et hoiame kuubikut alati niimodi käes, et esimesena lahendatav kiht asub all. Kuubiku orientatsiooni paigas hoidmine annab palju eeliseid. Esiteks on lihtne aru saada, kus juba lahendatud tükid on. Teiseks kui esimene kiht lahendatakse ära, siis ta on meil allpool ja me ei näe teda. Selle asemel me näeme kuubikul neid tükke, mis pole veel lahendatud, mis ongi need tükid, mis meile rohkem huvi pakuvad.

Rist

Mis on rist?

Esimese kihi lahendamise jaotame kaheks suureks sammuks. Lahendame kõigepealt esimese kihi ääred (rist) ja seejärel nurgad. Enne risti loomist peaksime endale selgeks tegema, mida me selle all mõtleme. Rubiku kuubiku lahendamisel tähendab rist ühte keskust, mille ümber on lahendatud neli ääretüki.

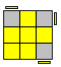
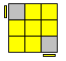
Näiteks siin on pealmisel kihil küll midagi ristilaadset. Samas ei ole ääretükid tegelikult õigetes kohtades. Kohe ees näeme, et punane-valge ristitükk asub valge ja rohelise keskuse vahel, mis pole õige.

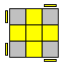
Korrektselt lahendatud rist näeks välja järgmine. Seal on näha, et iga valge ääretükk paikneb kahe keskuse vahel, mis klapivad tema värvidega (s.t iga valge ääretükk on lahendatud).

Siinkohal peaks mainima, et kuigi edaspidi toodud näidetes on alati lahendatud valge rist, pole tegelikult vahet mis värvi keskuse ümber risti ehitada. Tihti on mõne keskuse juures mingi osa ristist ette lahendatud. Seega soovitan soojalt ka teisi värve proovida

Risti lahendamine

Enne selle peatüki lugemist soovitan iseseisvalt üritada risti lahendada. On täiesti võimalik et saate sellega ise väga hästi hakkama, kui natuke vaeva näete. Kellel on veel abi vaja, siis lugege edasi.

Rubiku kuubiku lahendamismeetodid põhinevad Rubiku kuubiku kindlateks osadeks jagamisel. Need osad lahendatakse eraldi. Näiteks kiht-kihi haaval lahendades jagame kuubiku mõtteliselt kolmeks kihiks, mis lahendame ükshaaval. Samas saab ka lahendamise erinevaid etappe omakorda alametappideks jaotada.

Kõige lihtsam ja loomulikum viis risti lahendada on tükkhaaval. Meil on vaja lahendada neli ääretükki. Konkreetse tüki lahendamise saame soovi korral ka jaotada kaheks osaks.

• Esiteks toome tüki viimasesse kihti.
• Teiseks asetame ta alumisse kihti õigete keskuste vahele.

Järgnevalt vaatame läbi paar näidet valge risti lahendamisest.

1. Ääretükk asub ülemises kihis

Kui lahendatav ääretükk asub ülemises kihis, siis on teda väga lihtne lahendada.

1. Kõigepealt liigutame tüki õige keskuse kohale. Näiteks punase-valge ääretüki paigutame punase keskuse kohale.
2. Kui valge värv on suunatud ülesse, siis liigutame tüki alumisse kihti 180 kraadise pöördega.
3. Kui valge värv on suunatud küljele, siis hoiame kuubikut käes nii, et see kleeps on suunatud meie poole. Seejärel sooritame algoritmi U' R' F R

Vaata ka järgmist näidet risti lahendamisest, kus neli ääretükki asuvad ülemises kihis.

2. Ääretükk asub alumises kihis

Kui ääretükk asub alumises kihis, aga pole veel lahendatud, siis kõigepealt liigutame ta viimasesse kihti topeltpöördega.

Eelmise näite põhjal oskame juba lahendada ääretükki, mis paikneb viimases kihis. Illustreerime seda näitega.

3. Ääretükk asub keskmises kihis

Kui ääretükk asub keskmises kihis läheneme probleemile samamoodi nagu eelmises näites. Kõigepealt toome ääretüki viimasesse kihti. Seejärel paigutame ta õigesse kohta.

Et tuua ääretükk keskmisest kihist viimasesse keerame kuubikut käes, kuni uuritav tükk asub eesmisel küljel paremal. Viimasesse kihti toomiseks kasutame algoritme R U R' või F' U' F.

Näide.

Küsimused

1. Esitasime kaks erinevat algoritmi, et ääretükk keskmisest kihist ülemisse kihti tuua. Kas on vahet millist neist kasutada?
2. Olgu meil ääretükk ees paremal keskmises kihis. Miks me ei või teda viimasesse kihti tuua lihtsalt R liigutusega?

Kontrollige vastust 1. Nende algoritmi tulemusena satub ääretükk viimasesse kihti erinevas orientatsioonis. Üldiselt soovime paigutada tüki viimasesse kihti nii, et risti värvi kleeps oleks suunatud üles. Valge risti puhul oleks selleks valge kleeps. 2. Seda võib tegelikult teha, eeldusel et me sellega juba lahendatud ääretükke paigast ei nihuta. Näiteks järgmises näites rikub R liigutus risti ära.

Vaatame nüüd veel ühte näidet risti lahendamisest.

Esimese kihi nurgad

Nüüd kui oskame esimess

Viimane kiht

Rubiku kuubiku viimast kihti lahendame kahes osas. Esiteks tegeleme tükkide orientatsiooniga ja teiseks permutatsiooniga.

Viimase kihi orientatsioon

OLL (orientation of last layer) on Rubiku kuubiku viimase kihi lahendamise samm, mille lõpuks on kuubik ülalt vaadatuna sama värvi. Ehk kui viimaseks kihi keskuse tükk on kollane, siis on kõikide tükkide kollased kleepsud orientatsiooni sammu lõpuks üles suunatud.

• 
  Kuubik, mille viimase kihi orientatsioon on lahendatud.

Sellel sammul ei pööra me tükkide asukohale tähelepanu. Meid huvitab vaid nende orientatsioon.

Äärte orientatsioon

Äärte orienteerimiseks kasutame ühte väga lühikest algoritmi. Selleks on F (R U R' U') F' (sulud on vaid selleks, et algoritmi oleks lihtsam lugeda). Selle algoritmiga saate alati äärte orientatsiooni lahendatud. Enne näidete vaatamist proovige seda algoritmi ise kuubikule rakendada ja uurige mis juhtub.

Kui vaatate kuubikut pealtpoolt, peaks esinema üks kolmest olukorrast.

Pöörake tähelepanu vaid äärtele, nurkadega tegeleme hiljem. Tuletan ka meelde, et see pilt kujutab kuubikut pealt poolt vaadatuna. Kuubikut hoiate endiselt nii käes, et viimane kiht on üleval.

• 
  1.
• 
  2.
• 
  3.

• Kui teil on 1. pildi olukord, siis sooritage lihtsalt ees toodud algoritm: F (R U R' U') F'.
• Kui teil on 2. pildi olukord, siis sooritage sama algoritm kaks korda.
• Kui teil on 3. pildi olukord, siis sooritage algoritm ühe korra, tehke U2 pööre ning saate 2. pildil toodud olukorra.

Nurkade orientatsioon

Nurkade orientatsioon on veidi keerulisem kui äärte orientatsioon. Kui äärte jaoks oli meil kolm põhijuhtu, siis nurkade jaoks on neid seitse. Kõiki neid olukordi saab lahendada vaid ühe algoritmiga, kuid seda algoritmi peab mõnel juhul väga palju kordi sooritama.

Tavaliselt kasutatakse selleks algoritmi, mille nimi on sune (hääldus sama, mis ingliskeelsel sõnal soon). Algoritm on R U R' U R U2 R' . Seda on ka väga kerge meelde jätta. Lihtsalt jätke meelde, et ülemine kiht liigub päripäeva, päripäeva ja 2 korda päripäeva ning parem kiht liigub vahepeal korda-mööda päripäeva ja vastupäeva.

Sune keerab viimasel kihil kolme nurka päripäeva ning jätab puutumata nurga, mis asub ees vasakul. Seega kui saate seda algoritmi kasutades olukorra, kus vaid üks nurk on õige orientatsiooniga, siis saate selle algoritmiga ülejäänud nurgad ka õigesse orientatsiooni keerata. Samas ei ole alati selge kuidas seda algoritmi rakendama peaks.

Selle probleemi lahendamiseks on kaks ideed:

1. esiteks võib lihtsalt proovida sune rakendada kuni saab orientatsioon lahendatud;
2. teise variandina võib ära õppida iga nurkade OLL olukorra jaoks eraldi algoritmi.

Siin esitame kõik nurkade orientatsiooni olukorrda ja nende lahendusalgoritmid.

• 
  R U R' U' R U2 R' (sune)
• 
  R' U' R' U' R' U2 R
• 
  F (R U R' U')(R U R' U')(R U R' U') F'
• 
  (R U2) (R2 U') (R2 U') (R2 U2) R
• 
  (R2 D) (R' U2) (R D') (R' U2 R')
• 
  (Rw U R' U') (Rw' F R F')
• 
  F' (Rw U R' U') Rw' F

Selle asemel võite ka kõik lihtsalt sunega lahendada. Abiks on järgnev skeem:

Viimase kihi permutatsioon

Nüüd kui kõik tükid on õige orientatsiooniga, on aeg nad üksteise suhtes õigesti paigutada. Permutatsiooni tuvastame vaadates viimase kihi tükkide külgmisi kleepse. Kiirkuubijate seas viidatakse sellele sammule enamasti lühendiga PLL (permutation of last layer).

Esiteks tegeleme nurkadega.

Nurkade permutatsioon

• 
  Kuubik, mille viimase kihi nurkade permutatsioon on lahendatud.

Hea uudis on see, et nurkade permutatsiooni jaoks on ainult kaks erinevat olukorda. Halb uudis on see, et peab uue jälle uue algoritmi ära õppima.

Esiteks uurige, äkki on nurkade permutatsioon juba lahendatud. Proovige ülemist kihti keerata nii, et kõik nurgad paikneksid õiges kohas. Kui see on tehtav, siis on nurkade permutatsioon juba lahendatud. Kui ei, siis on kaks võimalust:

1. kaks kõrvuti asetsevat nurka on üksteise suhtes lahendatud;
2. sellist nurkade paari ei leidu.

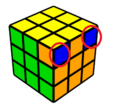
Kuigi need kõlavad keeruliselt on tegelt olukordada ära tundmine väga lihtne. Otsime lihtsalt külgede pealt nurkade paari, millel on sama külje peal sama kleeps.

• 
  Kuubik, mille kaks nurka on üksteise suhtes lahendatud.

Pildi pealt on näha, et kahel nurgal on ühe külje peal sama kleeps (sinine). Seega nad on üksteise suhtes lahendatud. Ehk tegemist on 1. juhuga. Sel juhul pöörame ülemist kihti nii, et lahendatud nurgad on taga ning sooritame järgmise algoritmi: x (R' U R') D2 (R U' R') D2 R2 x'.

Juhin tähelepanu, et x tähistab 90 kraadist pööret ümber x telje. Sisuliselt pöörake tervet kuubikut käes nii, et nüüd on teie poole suunatud külg, millele risti lahendasite.

Kui aga teil sellist üksteise suhtes lahendatud nurkade paari ei leidu, siis sooritage sama algoritm suvaliselt küljelt. Seejärel peaks kaks nurka paika minema ning saate 1. olukorra.

Äärte permutatsioon

Märkamatult oleme jõudnud kuubikulahendamisega finišisirgele. Viimane samm on äärte õigetesse kohtadesse paigutamine.

Selleks on meil algoritm R2 U (R U R' U') (R' U') (R' U) R'.

See algoritm liigutab kolme äärt päripäeva ringi. Tagumisel küljel paiknev äär jääb aga samasse kohta. Seega on strateegia lihtne. Me leiame lahendatud ääre ja keerame ülemist kihti, kuni see asub tagumisel küljel. Seejärel sooritame algoritmi. Kui sellist äärt pole, siis sooritame algoritmi suvaliselt küljelt.