Anorgaaniline Keemia/REDOKSREAKTSIOONID

Tin structures settled on a zinc by a redox reaction between Zinc and Tin Cloride.

A redox reaction is a reaction that occurs by the transfer of electrons from one species to another. Electron gain is called reduction and electron loss is called oxidation. The species that supplies electrons is the reducing agent (or ‘reductant’) and the species that removes electrons is the oxidizing agent (or ‘oxidant’). Oxidation then corresponds to an increase in the oxidation number of an element and reduction corresponds to a decrease in its oxidation number.

A redox reaction can be expressed as the difference of two reduction half-reactions.

Zn(s) + 2H⁺(aq) → Zn²⁺ (aq) + H₂(g)

2H⁺ (aq) + 2e^- → H₂(g)

Zn²⁺(aq) + 2e^- → Zn(s)

The oxidized and reduced species in a half-reaction constitute a redox couple. A couple is written with the oxidized species before the reduced, as in H⁺ /H₂ and Zn²+/Zn.

Standard potentials

The thermodynamic criterion of spontaneity is that, at constant temperature and pressure, the reaction Gibbs energy change, Δ_rG, is negative. The standard reaction Gibbs energy, Δ_rG°, is usually used. It is related to the equilibrium constant, K, through

Δ_rG°=−RT lnK

Because the overall chemical equation is the difference of two reduction half-reactions, the standard Gibbs energy of the overall reaction is the difference of the standard Gibbs energies of the two half-reactions. The half-reaction of the reduction of hydrogen ions were chosen to have Δ_rG°=0 at all temperatures.
Standard reaction Gibbs energies may be measured by setting up a galvanic cell, an electrochemical cell in which a chemical reaction is used to generate an electric current. The cathode is the electrode at which reduction occurs and the anode is the site of oxidation.
Standard conditions for an electrochemical cell are defined as follows:

• unit activity for each component in the cell;
• the pressure of any gaseous component is 1 bar (105 Pa);
• a solid component is in its standard state;
• the temperature is 298 K.
  

The potential difference of the cell composed of a hydrogen electrode and electrode of interest under standard conditions is named standard potential of the electrode. Its value can be converted to a reaction Gibbs energy:

Δ_rG = -nFE,

where n is the stoichiometric coefficient of the electrons transferred when the half-reactions are combined and F is Faraday’s constant (F = 96.48 kC/mol).

The standard potential of the H⁺/H₂ couple is zero at all temperatures.
For example, for reaction

Zn²⁺(aq) + 2e- → Zn(s)
E°(Zn²⁺, Zn) = -0.76 V

E_cell° for an overall reaction
2H⁺ (aq) + Zn(s) → Zn²⁺(aq) + H₂(g)
is the difference of the two standard potentials of the reduction half-reactions.
E_cell° =E°(H⁺,H₂) - E°(Zn²⁺, Zn) = 0 -(-0.76V) = +0.76 V

A reaction is favourable (in the sense K>1) if the corresponding standard cell potential is positive. Zinc has a thermodynamic tendency to reduce H⁺ ions under standard conditions. The same is true for any metal that has a couple with a negative standard potential.

The factors that contribute to the standard potential

The general half-reaction for M^z+ reduction M^z+(aq) + ze^- → M(s) can be represented as taking place in 3 steps:

1. M^z+(aq) → M^z+(g) dehydration/hydration (Δ_hG≈ Δ_hH)
   
2. M^z+(g) → M (g) ionisation (Δ_iG= −Σ(IE))
   
3. Me(g) → Me(s) sublimation/atomization (Δ_sG=-Δ_sH)
   

The thermodynamic cycle is simplified by ignoring the reaction entropy. Gibbs energy change for the half reaction than can be expressed as the sum of energy changes for the steps, and standard potential is:

E°=ΔG/zF°=(Δ_hH−Σ(IE)-Δ_sH)/zF

Cs+/Cs and Li+/Li couple

The variation of standard potential down Group 1 seems contrary to expectation based on electronegativities insofar as Cs+/Cs ( χ=0.79, E°=2.94 V) has a less negative standard potential than Li+/Li (χ=2.20, E°=-3.04 V) despite Li having a higher electronegativity than Cs. Lithium has a higher enthalpy of sublimation(Δ_sH=171 kJ/mol) and ionization energy(IE=526kJ/mol) than Cs (Δ_sH=79kJ/mol, IE=382kJ/mol), and in isolation this difference would imply a less negative standard potential as formation of the ion is less favourable. However, Li+ has a large negative enthalpy of hydration(Δ_{h Li}H=-520kJ/mol, Δ_{h Cs}H=-264kJ/mol), which results from its small size (its ionic radius is 90 pm) compared with Cs\+ (181 pm) and its consequent strong electrostatic interaction with water molecules. Overall, the favourable enthalpy of hydration of Li outweighs terms relating to the formation of Li+ (g) and gives rise to a more negative standard potential.

Na+, Na and Ag+, Ag couple

The value of E°(Na+, Na) = -2.71V may also be compared with that for E° (Ag+, Ag) = +0.80V. The (6-coordinate) ionic radii of these ions (r(Na) = 102 pm and r(Ag) = 115 pm) are similar, and consequently their ionic hydration enthalpies are also similar(Δ_{h Na}H=-406kJ/mol, Δ_{h Ag}H=-468kJ/mol). However, the much higher enthalpy of sublimation of silver(Δ_{s Ag}H=284kJ/mol, Δ_{s Na}H=109kJ/mol), and particularly its high ionization energy (IE_Ag=735kJ/mol, IE_Na=502kJ/mol), which is due to the poor screening by the 4d electrons, results in a positive standard potential.

The Nernst equation

To judge the tendency of a reaction to run in a particular direction at an arbitrary composition, it is needed to know the sign and value of Δ_rG at that composition.
Δ_rG= Δ_rG° + RT lnQ,

where Q is the reaction quotient:

aOx_A + bRed_B → a’Red_A + b’Ox_B Q=[Red_A]^a'[Ox_B]^b'/[Ox_A]^a[Red_B]^b

At equilibrium, Q = K. When evaluating Q and K, the quantities in square brackets are to be interpreted as the numerical values of the molar concentrations. For reactions involving gas-phase species, the molar concentrations of the latter are replaced by partial pressures. Both Q and K are dimensionless quantities. Considering that:
E_cell = -Δ_rG/nF and E_cell° = -Δ_rG°/nF
the Nernst equation is:

E_cell = E_cell°- RTlnQ/nF

A reaction is spontaneous if, under the prevailing conditions, E_cell>0, for then Δ_rG<0.

At equilibrium E_cell=0 and Q = K, so
lnK=nFE_cell°/RT

The influence of pH

For many reactions in aqueous solution the electrode potential varies with pH because reduced species of a redox couple are usually much stronger Brønsted bases than the oxidized species. For a redox couple in which there is transfer of n_e electrons and n_H protons

Ox + n_ee^- + n_HH⁺ → RedH_nH Q=[RedH_nH]/([Ox][H+]^H+) and

E = E°- (RT/n_eF) * ln([RedH_H]/[Ox][H⁺]^nH) = E°- (RT/n_eF) * ln([RedH_H]/[Ox]) + n_HRT ln([H⁺])/n_eF
If use ln[H⁺] = ln 10 log[H₊], pH = -log[H⁺] and define E’ as

E’= E°- (RT/n_eF) * ln([RedH_H]/[Ox]),

the potential of the electrode can be written as

E=E’- (n_HRT*ln10/n_eF)*pH
At 25°C

E=E’- ((0,059V)n_H/n_eF)*pH

The potential decreases as the pH increases and the solution becomes more basic.

Latimer diagrams

In a Latimer diagram (a reduction potential diagram) for an element, the numerical value of the standard potential (in volts) is written over a horizontal line connecting species with the element in different oxidation states. The most highly oxidized form of the element is on the left, and in species to the right the element is in successively lower oxidation states.

The Latimer diagram for chlorine in acidic solution, for instance, is

As many half-reactions involve H⁺ or OH^- ions and the reduction potential varies with pH the Latimer diagrams are appropriate only at the stated pH values (usually diagrams are given for pH=0 and pH=14).
The standard potential of a couple that is the combination of two other couples is obtained by combining the standard Gibbs energies, not the standard potentials, of the half-reactions.
ΔG_a+b= ΔG_a + ΔG_b
-nFE_a+b= -n_aFE_a–n_bFE_b, E°_a+b=(n_aE°_a+n_bE°_b)/(n_a+n_b)

Example. To calculate the value of E° for the HClO2/Cl2 couple in acidic aqueous solution the following two half-reactions are used: HClO2+2e-→HClO (E°=+1,7) and HClO+e-→1/2Cl2 (E°=+1,6). Their sum is the half-reaction for the required couple and E°=2*1,7+1,6/(1+2)=1,7

A species has a tendency to disproportionate into its two neighbours if the potential on the right of the species in a Latimer diagram is higher than that on the left.

Example. Thermodynamically HClO2 has a tendency to disproportionate into HClO and ClO2

Frost diagrams

Frost diagram for manganese

A Frost diagram (an oxidation state diagram) of an element is a plot of nE°(or ΔG° as ΔG°/F=nE°) for the couple X(N)/X(0) against the oxidation number, N, of the element. It shows how the Gibbs energies of formation of different oxidation states of an element vary with oxidation number.

Constructing of a diagramm

The (0,0) poit corresponds to the element is in its zero oxidation state.
In order to get other points coordinates the value E° should be taken for pair Xⁿ⁺/X⁰ where reduced form is in its zero oxidation state and multiplied by the oxidation number of oxidized form.

Example. Volt-equivalent value, n, for Mn2+ is 2, and for Mn2O is 4. 

Features of a Frost diagramm:

• 1.The most stable oxidation state of an element corresponds to the species that lies lowest in its Frost diagram.
  

Example. Mn2+ is the most stable oxidation state for manganese in acidic media.

• 2.The slope of the line joining any two points (tg α) is equal to the standard potential of the couple, the steeper the line, the higher the standard potential.
• 3.The oxidizing agent in the couple with the more positive slope is liable to undergo reduction.
• 4.The reducing agent of the couple with the less positive slope is liable to undergo oxidation.

Example. The steep slope connecting H3MnO4 to lower oxidation numbers shows that this substation is a good oxidizing agent under standard conditions.

• 5.A species in a Frost diagram is unstable with respect to disproportionation if its point lies above the line connecting the two adjacent species.

Example. Because Mn3+ lies above the line joining Mn2+ to MnO2, it should disproportionate into these two species. The chemical reaction is 2Mn3+(aq)+2H2O(l) → Mn2+(aq) + MnO(s) + 4H+(aq)

• 6.Two species will tend to comproportionate into an intermediate species that lies below the straight line joining the terminal species. A substance that lies below the line connecting its neighbours in a Frost diagram is inherently more stable than neighbours because their average molar Gibbs energy is higher and hence comproportionation is thermodynamically favourable.

Pourbaix diagrams

Simplified Pourbaix diagramm for iron

A Pourbaix diagram (an E-pH diagram) is a map of the conditions of potential and pH under which species are stable in water.
A horizontal line separates species related by electron transfer only (redox reaction), a vertical line separates species related by proton transfer only, and sloped lines separate species related by both electron and proton transfer.
The simplified Pourbaix diagram for iron involves next reactions:
1) Fe³⁺(aq) + e^- → Fe²⁺(aq) E°= 0.77V
This reaction does not involve H⁺ ions, so its potential is independent of pH and hence corresponds to a horizontal line on the diagram. If the environment contains a couple with a potential above this line, then the oxidized species, Fe³⁺ , will be the major species. Hence, the horizontal line towards the top left of the diagram is a boundary that separates the regions where Fe³⁺ and Fe²⁺ dominate.
2) Fe³⁺(aq) + 3H₂O(l) → Fe(OH)₃(s) + 3H⁺ (aq)
This reaction is not a redox reaction, so it is insensitive to the electric potential in its environment and therefore is represented by a vertical line on the diagram. However, this boundary does depend on pH, with Fe³⁺(aq) favoured by low pH and Fe(OH)₃(s) favoured by high pH.
3) Fe(OH)₃(s) + 3H⁺(aq) + e^-→ Fe²⁺(aq) + 3H₂O(l)
For this reaction the slope of potential against pH is n_H/n_e=-3.

The stability field of water

The blue sloping lines on a Pourbaix diagramm defining the upper and lower limits of thermodynamic water stability. The lines are the potentials for the O₂/H₂O and H⁺/H₂ couples, respectively.
Water may act as an oxidizing agent, when it is reduced to H₂:
H₂O(l) + e^- →1/2H₂(g) + OH^- (aq)
For the equivalent reduction of hydronium ions in water at any pH (and partial pressure of H₂ of 1 bar) the Nernst equation gives
H⁺(aq) + e^- →1/2H₂(g) E=-0,059V pH
Water may also act as a reducing agent, when it is oxidized to O₂:
2H₂O(l) → O₂(g) + 4 H⁺ (aq) + 4e^-
When the partial pressure of O₂ is 1 bar, the Nernst equation becomes
E= 1.23V - 0.059V pH
A reducing agent that can reduce water to H₂ rapidly, or an oxidizing agent that can oxidize water to O₂ rapidly, cannot survive in aqueous solution. The stability field of water is the range of values of potential and pH for which water is thermodynamically stable.

Ellingham diagram

Ellingham diagram for the reduction of some metall oxides

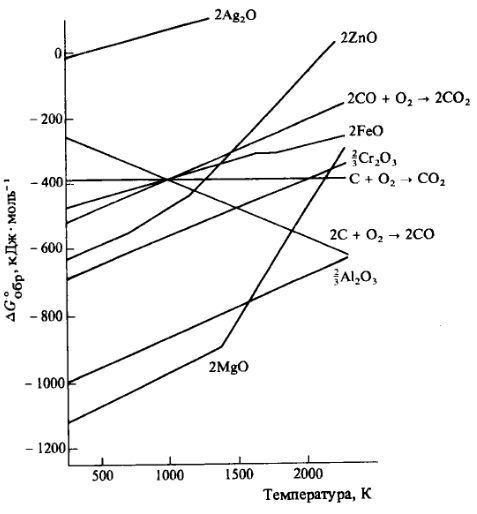
An Ellingham diagram is a graph of Δ_rG° against the temperature. It summarizes the temperature dependence of the standard Gibbs energies of formation of metal oxides and is used to identify the temperature at which reduction by carbon or carbon monoxide becomes spontaneous.

To achieve a negative Δ_rG° for the reduction of a metal oxide with carbon or carbon monoxide, one of the following reactions

a)C(s) + O₂(g) → CO(g)
b)1/2C(s) + 1/2O₂(g) → 1/2CO₂
c)CO(g) + 1/2O₂(g) → CO₂(g)

must have a more negative Δ_rG° than a reaction

xM(s or l) + 1/2O₂ → M_xO

under the same reaction conditions.
For constructing of an Ellingham diagramm the equation Δ_rG° = Δ_rH° - TΔ_rS°
is used and the fact that the enthalpy and entropy of reaction are, to a reasonable approximation, independent of temperature. That being so, the slope of a line in an Ellingham diagram should therefore be equal to Δ_rS° for the relevant reaction.
Using of the diagramm:

• For temperatures at which the C/CO line lies below the metal oxide line, carbon can be used to reduce the metal oxide and itself is oxidized to carbon monoxide.
• For temperatures at which the C/CO₂ line lies below the metal oxide line, carbon can be used to achieve the reduction, but is oxidized to carbon dioxide.
• For temperatures at which the CO/CO₂ line lies below the metal oxide line, carbon monoxide can reduce the metal oxide to the metal and is oxidized to carbon dioxide.